适当的样本量是保证体外诊断临床试验能得到准确评价的必要条件。如果研究目的是评价某指标的诊断价值,样本量计算根据诊断指标的不同而不同。如果诊断指标是灵敏度,根据灵敏度和设定的精确度可以估算所需的"有病"例数;如果诊断指标是特异度,根据特异度和精确度估算出的是"无病"的例数;如果诊断指标是ROC曲线下面积,根据ROC曲线下面和特定的精确度可以计算出"有病"的例数
采用统计学公式进行样本量估算的相关要素一般包括评价指标的预期值,1类错误,2类错误概率以及预期的受试者脱落剔除率等
一般情况下,1类错误概率α设定为双侧0.05或单侧0.025,2类错误概率β设定为不大于0.2
样本量是根据事先确定的因素来估计的,影响样本量大小的因素很多,常见有以下几种:
- 假设检验的方向
- 一类错误和二类错误
- 效应值大小
- 其他因素
从下面的描述中大致可看出,IVD的指导原则中对于样本量估计主要涉及假设检验方向
以下部分参考《体外诊断试剂临床试验指导原则(征求意见稿)》
定性检测的样本量估算
评价指标有确定的临床可接受标准时,需正常产品评价指标不低于临床可接受标准。此时可采用单组目标值法样本计算公式估算最低的样本量,公式参考如下:
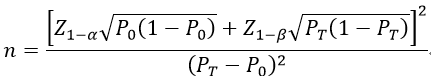
其中,Z1-α和Z1-β为显著性水平和把握度的标准正态分布中的1-α和1-β对应的分位数。P0为评价指标的临床可接受标准,PT为评价指标的预期值
比如:
估计某试验产品,对于特异性,假设预期临床特异性为95%,根据临床对此类检测试剂的特异性要求,设定特异度目标值为90%,把握度(1-β)为0.8,单侧检验α=0.025,则该试验所需样本量为
Z_alpha <- qnorm(p = 0.975, lower.tail = T)
Z_beta <- qnorm(p = 0.8, lower.tail = T)
P0 <- 0.9
Pt <- 0.95
n <- (Z_alpha * sqrt(P0 * (1 - P0)) + Z_beta * sqrt(Pt * (1 - Pt)))^2 / (Pt - P0)^2
> n
[1] 238.0332约为238例样本
对于临床试验的参数估计中只保证评价指标可信区间的宽度满足期望值,而无目标值的情况,则可采用如下公式:
![]()
其中,Z1-α/2为显著性水平的标准正态分布中的1-α/2对应的分位数,P为评价指标的预期值,Δ为P的允许误差大小,一般取P的95%可信区间宽度的一半,常用的取值为0.05-0.1
比如:
估计某试验产品,对于灵敏度,假设预期临床总灵敏度为85%,simple Asymptotic置信区间下限为80%,则该试验所需样本量为(根据上述公式):
> qnorm(0.975)^2 * 0.85 * (1 - 0.85) / 0.05^2
[1] 195.9144即约为196例样本
换一个例子:
估计某试验产品,对于灵敏度,假设预期临床总灵敏度为77%,Wilson-score置信区间下限为70%(说明允许误差取值为0.07),则该试验所需样本量为
这个例子中用了wilson-score置信区间,与上个例子的simple Asymptotic置信区间不同,因此公式无法使用,这里可以使用PASS软件的Confidence Interval for One Proportion模块来计算,其中包括了上述例子的Simple Asymptotic方法和Wilson Score方法
从其文档可知,对于此类sample size的计算,都是基于计算confidence interval的公式转化而来,因此若知道不同方法的计算公式,即可编写函数来计算sample size,如:

从上可看出,当方法选Simple Asymptotic时,经公式转化后即可得上述第一个例子所对应的公式;对于Wilson Score的方法,按照常规公式转化计算n参数比较困难,此时可用R的一些函数(uniroot或者pracma::regulaFalsi)来解方程求解样本量n
sampleSize <- function(n, z, p, limit){
t1 <- 1/2 * (2 * n * p + z^2) / (n + z^2)
t2 <- 1/2 * z * sqrt(z^2 + 4 * n * p * (1 - p)) / (n + z^2)
return(t1 - t2 - limit)
}
z <- qnorm(0.975)
p <- 0.77
limit <- 0.7
N <- uniroot(sampleSize, c(1, 1000), tol = 1e-08, z = z, p = p, limit = limit)
str(N)
# pracma::regulaFalsi(sampleSize, 1, 1000, z = z, p = p, limit = limit)即约为165例样本
定量检测的样本量估算
对于定量检测,亦可针对适当的评价指标(如Bland-Altman分析中的平均误差,回归分析中的回归系数和截距等),选择适宜的统计学方法,进行样本量估算
比如:
假设考核试剂与对比试剂间的预期相关系数为0.986,双侧检验alpha=0.05,区间宽度为0.018,则置信区间下限为0.975,则该试验所需样本量为:
注意:这里计算样本量的方式不要跟Power and Sample Size for Correlation Testing搞混,这里是需要在保证相关系数下限(即0.975的前提下),达到预期相关系数0.985时所需要的样本量
这个计算方式可以使用PASS软件的的Confidence Interval for Pearson's Correlation模块来计算
从该模块的文档可知,其是参考这篇文献:Sample size estimation for correlations with pre-specified confidence interval
逻辑思路可参考代码:
CIxcorr <- function(alpha, corr, N) {
# Computes a confidence interval for a Pearson correlation
# Args:
# alpha: alpha level for (1-alpha) confidence
# corr: value of correlation
# N: sample size
# Returns:
# confidence interval
Z <- qnorm(1 - alpha/2)
# Z = 1.9599640 for 95% CI
se <- sqrt(1/((N - 3)))
zr <- log((1 + corr)/(1 - corr))/2
LL0 <- zr - Z*se
UL0 <- zr + Z*se
LL <- (exp(2*LL0) - 1)/(exp(2*LL0) + 1)
UL <- (exp(2*UL0) - 1)/(exp(2*UL0) + 1)
CI2w <- UL - LL
# CI width CI2w output added to Bonett’s CIcorr R-function
CI <- c(LL, UL, CI2w)
return(CI)
}
CIxcorr(0.05, 0.986, 45)
sizeCIcorr <- function(alpha, corr, CI2w) {
# Computes sample size required to estimate a correlation with desired precision
# Args:
# alpha: alpha level for 1-alpha confidence
# corr: planning value of correlation
# CI2w: desired confidence interval width
# Returns:
# required sample size
z <- qnorm(1 - alpha/2)
n1 <- ceiling(4*(1 - corr^2)^2*(z/CI2w)^2 + 3)
zr <- log((1 + corr)/(1 - corr))/2
se <- sqrt(1/(n1 - 3))
LL0 <- zr - z*se
UL0 <- zr + z*se
LL <- (exp(2*LL0) - 1)/(exp(2*LL0) + 1)
UL <- (exp(2*UL0) - 1)/(exp(2*UL0) + 1)
N <- ceiling((n1 - 3)*((UL - LL)/CI2w)^2 + 3)
return(N)
}
sizeCIcorr(0.05, 0.986, 0.018)以上为诊断试剂试验中一些常见的样本量计算方法,及其代码实现方法,整理做个笔记,仅供参考哈
若对其他的样本量计算方法感兴趣,可查看这篇文档:样本容量估计
参考资料
https://www.statsdirect.com/help/sample_size/correlation.htm
https://rdrr.io/cran/seqtest/man/size.cor.html
https://zhuanlan.zhihu.com/p/24631883
http://blog.sina.com.cn/s/blog_59ee51930100cqpy.html
http://www.360doc.com/content/17/0808/16/12656249_677601527.shtml
https://rstudio-pubs-static.s3.amazonaws.com/153235_a0277930a4924e46af765f4bbba3cdd6.html
https://blog.csdn.net/woodcorpse/article/details/106846784
https://www.osmundacn.com/news/newsinfo/id/1043.html
本文出自于http://www.bioinfo-scrounger.com转载请注明出处