蛋白质组学在现在众多组学中属于起步较晚的组学之一,一般跟代谢组并列提起,因为都是通过质谱仪进行检测(虽然代谢组不一定要用质谱)。我们通过质谱下机数据,然后经过软件进行图谱分析(查库),然后获得肽段/蛋白的丰度值,接下来可能就跟RNA-Seq等NGS数据一样,需要在蛋白表达谱(虽然由于仪器的限制,并未能检测到全部低丰度蛋白,鉴定到的蛋白数目还是处于N千数量级)中筛选出丰度发生显著变化的蛋白(这也就是常说的比较蛋白组学) RNA-Seq相比蛋白组发展较早,从芯片到NGS测序,其差异分析流程经过众多学者的完善趋于成熟;而蛋白组,根据其检测方法的不同,外加一些谱图分析软件的差异,并未能向NGS那样有着统一的规范输出结果。从一些蛋白组应用相关的文献来看,还处于较为简单的分析,比如T检验;这里并不是说T检验不好,而是从现在普遍生物学重复只做3个的现象来看,T检验的效应还是不够的吧?
我之前在一篇博文Differential expression in proteomics中简单整理了下最近几年发表关于蛋白组差异分析方法的文献,我整理的还是有偏差的,我只对蛋白组Label-free技术相关文献做了整理,而iTRAQ技术的则未关注(这是因为我觉得iTRAQ实在有点贵,不如label-free应用范围广,特别是当临床上百样本的时候)。
一般来说,现在蛋白组原始数据的采集分为DDA( Data-dependent acquisition)和DIA( Data-independent acquisition),Label-free技术的蛋白定量分析属于DDA,差不多就是shutgun原理;质谱仪在数据采集时先采集MS1数据,再采集N次MS2数据;因此Label-free的定量分析时出现了两种策略:第一种是基于MS2数据进行定量,也就是文献中说的Spectra Count,其一般符合泊松分布,因其后续差异分析可以参照NGS的RNA-seq分析的一些方法,比如DESeq2,edgeR等;第二种是基于MS1数据进行定量,计算每个肽段在谱图上的积分,也就是先通过MS1数据识别肽段,然后图形积分计算丰度,其在一些文献中普遍认为符合正态分布(个人觉得蛮勉强的),因此后续分析一些文献建议类似于芯片分析的一些方法,如T检验,limma等。
除了上述几个思路外,在最近的一篇博文一个R包的故事中提到MSstats作者在对蛋白组定量数据处理时,采用了一种完全不同于上述方法的一种的思路,其整理了每个Protein Group下所有肽段的丰度值,当其对同一个Protein Group在不同样本处理下进行差异分析时,并不是以Protein Group的丰度作为数据(因为一些定量软件不仅会给出每个肽段的丰度值,并用其算法得出每个Protein Group的丰度),而是类似将同一个Protein Group下每个肽段的丰度值看做一次'取样',比如如果某个Protein Group下,样本A有20个肽段,样本B有15个肽段,那么根据其logsum t-test算法,则T检验的自由度则为33。。是不是很独特的思路,其实有类似思路的文献,但见识的比较少。。
其实在做差异分析之前,还有一个步骤也是需要值得注意的,那就是需不需要进行空值填充,这是Label-free技术的缺陷所导致。一般在Label-free定量结果会看到不少蛋白在一些样本中的丰度值是缺失的,这很普遍。一些文献是采用过滤策略,比如大于50%样本有值的Protein Group保留(这在一些芯片分析过滤中比较常见);一些文献则会采用补空策略,比如用Multiple imputation算法等,但是由于label-free空值产生原因的不确定性,因此单一的补空算法无法准确对应到每个空值,因此有些研究者发现补空虽然能增加灵敏度,但会增加假阳性
下面我结合上述文献结论,以一个Label-free数据为例,分别使用T检验,Limma以及MSstats等方法进行蛋白组的差异分析
测试数据下载:labelfree.csv
首先做一步过滤处理,以50%原则过滤掉缺失值较多的Protein,这步主要针对后续T检验和limma的预处理,而MSstats则有其默认的预处理方式
library(ggplot2)
library(dplyr)
data <- read.csv(file = "labelfree.csv", sep = ",", header = T, row.names = 1)
rm <- apply(data, 1, function(x){
sum(x == 0) > 3
})
df <- data[!rm,]
> nrow(df)
[1] 5325接着则是做log转化,这步有没有必要呢?Label-free技术是用峰谱积分计算丰度的,其丰度的数量级在10的7次到10的11次不等,从下面每个样本的均值和标准差可看出,丰度值数据分布非常离散
Mean <- apply(df, 2, mean)
SD <- apply(df, 2, sd)
> Mean
A1 A2 A3 B1 B2 B3
2366243926 2351546722 2165457844 2175212680 2708233812 2290120209
> SD
A1 A2 A3 B1 B2 B3
13098498790 14392930144 14179115278 11151997873 12092333164 10344859562那么做log转化有什么用呢,一般作用为消除异方差;减少自变量数量级不一致的情况;使非线性变量关系转化为线性关系;最主要的还是为了使数据的呈现方式接近我们所希望的假设,从而更好的进行统计推断(以上来自知乎)
下面左边是原始数据AB两组的散点图,右边是做了对数转化后的
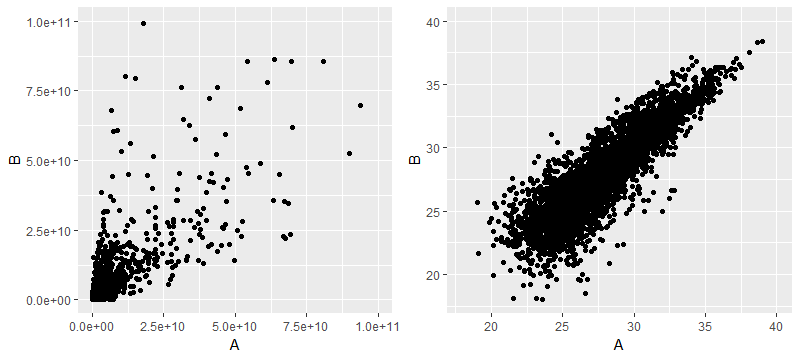
那么后续差异分析是用log转化后的数据还是原始数据呢,对于limma和MSstats两个软件来说,是必须做对数转化(其实前者是默认已经做了log转化的数据作为输入,而后者则是根据参数来设定如何做log转化,总之两者的差异分析结果都是做了log转化后的数据所产生的)。但T检验则是用哪个数据作为输入呢,因为统计推断T检验是比较两个样本均值是否有差异,但对做了log转化后的数据做T检验则不是比较算数平均数了,而是几何平均数,至少还算有明确的含义?
引用一位小伙伴对对数转化的理解,我觉得蛮有道理的
T检验或者方差分析之类的有参检验需要数据符合方差齐性,一般随着实验的进行,由于仪器或者人工操作,误差有可能会越来越大,会导致数据波动越来越大。这个时候可以用对数变换把方差变大的趋势给调回来
T检验
在做Two-Sample T检验前,需要样本总体符合正态分布,并且方差齐性,以测试数据为例(未做对数转化),先做个F检验
fvalue <- apply(df, 1, function(x){
a <- factor(c(rep("A",3), rep("B",3)))
var.test(x~a)
})
>sum(unlist(lapply(fvalue, function(x){
x$p.value > 0.05
})))
[1] 4605可看出5325个蛋白有4605个是方差齐性的
接下来用t.test函数做成组T检验,双尾(默认),方差不齐性的用var.equal = FALSE
pvalue <- apply(df, 1, function(x){
a <- factor(c(rep("A",3), rep("B",3)))
fvalue <- var.test(x~a)
if (fvalue$p.value > 0.05){
t.test(x~a, var.equal = T)
}else{
t.test(x~a, var.equal = F)
}
})
result_ttest <- data.frame(ID=row.names(df),
Pvalue = as.numeric(unlist(lapply(pvalue, function(x) x$p.value))),
log2FC = log2(as.numeric(unlist(lapply(pvalue, function(x) x$estimate[1]/x$estimate[2]))))
)
> sum(result_ttest$Pvalue < 0.05 & abs(result_ttest$log2FC) > 1)
[1] 704可看出差异蛋白数目为704个;如果是预处理时做了对数转化的话,代码同上(其中有略微区别,logFC是作相减,而不是上面代码的相除),结果符合相同的阈值的差异蛋白有694个
Limma
Limma就比较熟悉了,如果就测试数据两组比较而言,limma需要先做log2转化,然后设定分组矩阵,最后用线性模型拟合再用Empirical Bayes test求出检验的P值
library(limma)
df1 <- log2(df + 1)
group_list <- factor(c(rep("A",3), rep("B",3)))
design <- model.matrix(~group_list)
colnames(design) <- levels(group_list)
rownames(design) <- colnames(df1)
fit <- lmFit(df1, design)
fit <- eBayes(fit, trend=TRUE)
result_limma <- topTable(fit, coef=2,n=Inf)
>sum(result_limma$P.Value < 0.05 & abs(result_limma$logFC) > 1)
[1] 952Limma的差异蛋白数目就相比以上就略多了,满足阈值的有952个
MSstats
我按照之前博文一个R包的故事中的代码(做了略微的修改),对测试数据的原始数据进行了分析(因为MSstats包可以对Maxquant结果的最原始数据开始处理),分析过程这里不列出了(主要代码有点长。。。),结果文件可看MSstats_DEP.csv,结果满足阈值的差异蛋白有513个
Summary
其实我为什么要挑选这几种方法呢,因为一篇发表于2017年Briefings in Bioinformatics期刊的一篇文章比较过上述3种方法外加Generalized linear model with a gamma distribution(GLM-Gamma)方法对label-free数据的差异蛋白分析的结果,最终结果是Limma的Empirical Bayes test在低样本重复的情况下相比其他优势非常明显,随着样本重复数的增加,优势才会有略微缩小(总之作者认为limma对现在的label-free数据结果来说,相比其他方法,最佳)
最后将上述对数转化的T检验的p值做个多重检验(FDR),跟Limma和MSstats的adj.pavlue(校正后的P值)做个VENN图看看交集如何
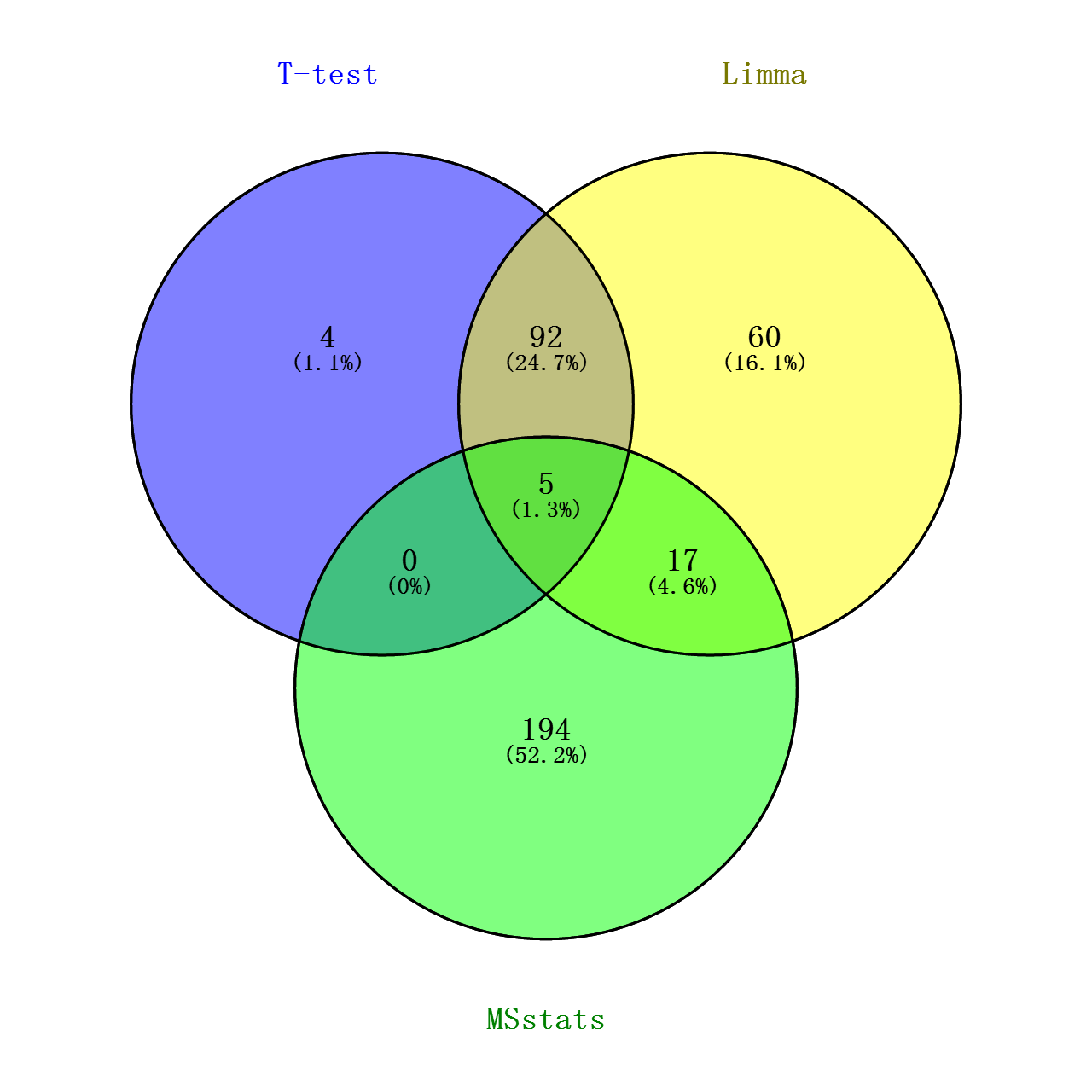
从图中可看出,Limma和T检验的覆盖度较好,可能由于这两种分析方式过程以及思路比较近似吧(都是默认蛋白水平的丰度值都符合正态分布),但limma在一些地方处理的比T检验更加好点(可能是由于limma在了线性拟合的缘故?),比如当一个样本丰度均为0,而另一样本丰度各个重复的丰度值偏差较大,这种情况T检验的效用比较糟糕,FDR值能难达到阈值,但这种情况,我觉得可以认为这个Protein Group在两个样本中表达是有差异的!!!至于MSstats,我不确定是否是我没有完全了解其用法,使得这方法筛选出来的差异蛋白跟其他两种相差较大(理论上按照文献中所展示的,不应该是这样的,但是那文献也没给出其计算的具体过程。。。),根据其R包代码,其分析过程的思路确实跟其他的方法有点不同。。。
本文出自于http://www.bioinfo-scrounger.com转载请注明出处